1.3.1 負載能力
成型軌導軌的負載能力由負載能力值表示。這些數值提供了選擇產品的基礎, 並依據 DIN ISO 14728-1(動態負載能力)和 DIN ISO 14728-2(靜態負載能力)進行計算。
負載能力表示導軌在產生永久損壞之前可以承受的力或負載。 負載能力的大小由以下因素決定:
- 負載滾動元件列數
- 每列負載滾動元件的數量
- 滾動元件直徑
- 滾動元件長度(滾柱適用)
- 接觸角
- 材料
- 軌道表面硬度
SCHNEEBERGER MONORAIL 導軌可以承受來自各個方向的力以及繞各軸的力矩。 負載能力分為動態負載能力和靜態負載能力兩種類型。

Forces and moments on the carriage
作用於滑座上的力與力矩
符號說明:
力矩(Moments)
負載能力(Load Capacity)
負載能力類型
動態負載能力 C
適用於運動中的導軌系統,用於計算使用壽命。
靜態負載能力 C0
適用於靜止或緩慢移動的導軌系統,用於評估最大允許負載。
負載能力值始終與單一滑座的負載能力相關。在一軸上使用多個滑座時, 負載能力不會倍增,因為剛性應用不允許負載在滑座間均勻分配。
重要提示
由於實際負載分配的不均勻性,當設計包含多個滑座時, 應考慮使用適當的安全係數進行計算。各產品的負載能力數值請參閱產品規格表。
1.3.2 動態負載能力 C
動態負載能力 C 定義為恆定負載,滾動接觸可以承受此負載達到 100,000 公尺的行程壽命。 對於計算滾動元件接觸的使用壽命,這是必需的關鍵數據。
壽命計算
滾動接觸的使用壽命可使用以下公式計算:
L = (C / P)p × 100,000 m
L = 行程壽命(公尺)
C = 動態負載能力(N)
P = 等效動態負載(N)
p = 壽命指數(滾珠 = 3,滾柱 = 10/3)
不同行程壽命的動態負載能力換算
SCHNEEBERGER 目錄中的動態負載能力 C 是以 100,000 公尺行程壽命(C100)為基準。 若需要以 50,000 公尺行程壽命為基準的數值,可使用以下換算公式:

Conversion of dynamic load capacity
動態負載能力換算公式
C50 = 1.23 × C100(滾珠導軌)
C50 = 1.26 × C100(滾柱導軌)
1.3.3 靜態負載能力 C₀
靜態負載能力 C₀(N)是 SCHNEEBERGER MONORAIL 導軌設計中的重要特性參數。 它用於驗證靜態安全係數。
根據 DIN ISO 14728-2 標準的定義,靜態負載能力 C₀ 是指在滾動元件與軌道接觸面產生 相當於滾動元件直徑 0.0001 倍的塑性變形時所對應的力。
靜態負載能力標示了導軌在靜止或緩慢運動時的負載極限。 在運行過程中,必須確保導軌不會承受超過靜態負載能力的力。 這同樣適用於短時間的事件,例如振動或衝擊。
重要注意事項
即使是短暫的振動或衝擊負載,也必須確保不超過靜態負載能力。 超過此限制可能導致滾動元件和軌道產生永久性變形,影響導軌的性能和精度。
靜態安全係數 S₀
靜態安全係數 S₀ 是防止滾動元件和軌道產生不允許的永久變形的保護值。 它定義為靜態負載能力 C₀ 與靜態等效力 P₀ 的比值:

Static safety factor S₀
靜態安全係數公式
S0 = C0 / P0
S0 = 靜態安全係數
C0 = 靜態負載能力(N)
P0 = 靜態等效力(N)
P₀ 的確定
對於 P₀,必須考慮作用於滾動接觸面的實際力。 滾動接觸面變形的決定性因素是最高振幅,這種振幅也可能在很短的時間內發生。
建議的安全係數
根據需求和運行條件,建議遵守以下靜態安全係數 S₀ 的最小值:
| 運行條件 | 建議 S₀ |
|---|---|
| 最小振動的正常運行 | ≥ 1.5 |
| 中等交變負載和振動 | ≥ 2.0 |
| 高衝擊負載和振動 | ≥ 3.0 |
| 高動態應力、高衝擊負載和振動 | ≥ 5.0 |
設計建議
具體計算方法請參閱第 4.10 節 - 計算與選型。 在實際設計中,應根據應用的具體運行條件選擇適當的安全係數。
1.3.4 靜態與動態力矩
允許的靜態力矩 M₀ 是指在滑座上產生相當於靜態負載能力 C₀ 的負載的力矩。 同樣地,允許的動態力矩 M 對應於動態負載能力 C。
允許的動態力矩對於導軌設計至關重要,特別是在滑座承受橫向力矩 MQ 和縱向力矩 ML 負載方面。橫向和縱向力矩會增加導軌的整體負載, 因此在計算使用壽命和靜態安全係數 S₀ 時必須相應考慮。詳見第 4.10 節 - 計算與選型。
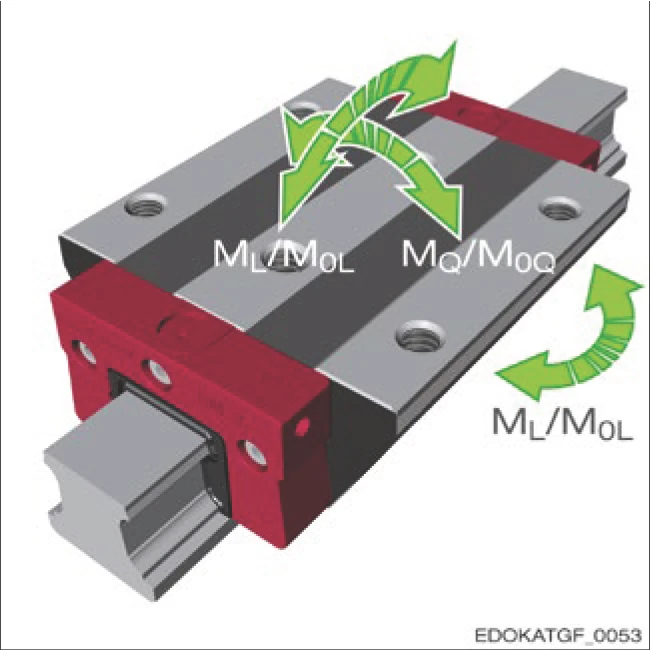
Moments on the carriage
作用於滑座上的力矩
力矩符號說明:
動態力矩
靜態力矩
縱向力矩 ML
允許的縱向力矩 ML 的大小主要取決於每列滾動元件的數量, 因此也取決於滑座的長度。長滑座比短滑座能夠承受更高的力矩。 在此過程中,各滾動元件的負載從外側向滑座中心分布。
縱向力矩 ML / M0L
繞導軌縱向軸旋轉的力矩。力矩大小取決於滑座長度和每列滾動元件數量。
橫向力矩 MQ / M0Q
繞導軌橫向軸旋轉的力矩。力矩大小取決於軌道間距和幾何配置。
橫向力矩 MQ
除了滑座長度外,軌道間距對於允許的橫向力矩 MQ 的大小也至關重要。 在所謂的 O 型幾何結構中,軌道間距比 X 型幾何結構的導軌更大。 詳見第 1.2 節 - 成型軌導軌的結構。
靜態橫向力矩 M0Q 的限制
靜態橫向力矩 M0Q 僅與滾動接觸的變形有關。 然而,成型軌導軌的最大允許橫向力矩也受到滑座和導軌螺絲連接的限制。 詳見第 4.11.7 節 - 導軌安裝 - 允許的拉力和橫向扭矩。
SCHNEEBERGER MONORAIL 的力矩特性
在 SCHNEEBERGER MONORAIL 導軌中,四條軌道以 90° 角相互配置。 這使得縱向力矩在橫向軸(ML)和垂直軸周圍具有同樣高的負載能力。
由於導軌採用 O 型幾何結構,實現了較大的軌道間距, 因此在縱向軸周圍的力矩(MQ)具有較高的負載能力。 各產品的具體數值可在 SCHNEEBERGER MONORAIL 和 AMS 產品目錄中查閱。
設計要點
- 長滑座(B、D 和 G 型)由於具有大量負載滾動元件,在力和力矩負載下的剛性表現最佳
- 橫向和縱向力矩會增加導軌的整體負載,必須在計算使用壽命時考慮
- 螺絲連接強度可能限制最大允許橫向力矩
1.3.5 負載方向
SCHNEEBERGER MONORAIL 和 AMS 產品目錄中的靜態(C₀)和動態(C)負載能力 是針對拉伸/壓縮/側向力的負載方向指定的。

Load directions at different angles
不同角度的負載方向(0°、90°、180°、270°)
負載能力與角度的關係
如果導軌在不同角度下承受負載,負載能力會降低。原因在於內部的力吸收方式。 理想情況下,力由 2 條軌道吸收。在最壞的情況下,當負載角度低於 45° 時, 只有一條軌道承受負載。
45° 負載方向的影響
負載能力降至原始值的約 70%
使用壽命降至約 30%

Influence of the direction of force on the service life: Roller guideway MR (red) and ball guideway BM (yellow)
力的方向對使用壽命的影響(%):滾柱導軌 MR(紅色)和滾珠導軌 BM(黃色)
對使用壽命的影響
SCHNEEBERGER MONORAIL 導軌的負載能力和使用壽命取決於負載方向。 在計算使用壽命時,需要使用組合等效力 P 來考慮這一因素。
力的分解
在幾何上,對於傾斜的力方向,根據下圖所示的總負載 Fres, 水平力分量 FY 和垂直力分量 FZ 通過向量加法累加作用於滑座。

Vector addition of the horizontal FY and vertical FZ force components for the total load Fres
總負載 Fres 的水平 FY 和垂直 FZ 力分量的向量加法
等效力公式
相反地,給定等效力 P,力分量通過以下公式進行代數相加:

Equivalent force formula
等效力公式
P = |FY| + |FZ|
P = 等效力
FY = 水平力分量(Y 方向力)
FZ = 垂直力分量(Z 方向力)
因此,對於不同於主方向的力,動態等效力始終大於作用於導軌的實際力。 這種方法使得在使用壽命公式中始終可以使用動態負載能力 C, 同時考慮到傾斜負載方向的負載能力降低及其相關的使用壽命減少。 詳見第 4.10 節 - 計算與選型。
使用壽命公式

Service life formula
標稱使用壽命公式
Lnom = a1 × (C / P)q × 100 km
Lnom = 標稱使用壽命
C = 動態負載能力
P = 等效力
a1 = 使用壽命調整係數
q = 使用壽命計算指數(滾柱 = 10/3,滾珠 = 3)
傾斜負載的使用壽命損失
傾斜負載導致的使用壽命損失可能很顯著,因為計算中包含比值 C/P, 其指數 q ≈ 3。在最壞的情況下,當作用力角度低於 45° 時, 與主力方向負載相比,使用壽命約減少 2/3。
設計建議
因此,在設計軸時務必確保根據主要負載方向配置導軌, 以實現最長的使用壽命。
負載配置原則
基本上,導軌應配置為使發生的力盡可能均勻地分布在滑座上, 且主負載作用在拉伸/壓縮方向。這樣的優點是力可以直接被導軌吸收, 並通過固定螺絲轉移到周圍結構。高側向力在某些情況下會產生作用於導軌的力矩, 只能通過連接結構中的額外定位面傳遞,這會產生額外的成本。