4.8 使用壽命

4.8.1 原理 Principles

4.8.1 原理

對精度等級、表面質量和短加工時間的要求不斷提高。這就是為什麼現代機械結構中的線性導軌越來越多地由允許的彈性變形決定。

因此，為滾柱導軌的尺寸設定了以下階段：

• 確定外部力和力矩
• 將力和力矩分配到各個滑塊上
• 確定預壓和變形
• 計算使用壽命
• 計算靜態可信賴性係數

使用壽命可能受材料疲勞的限制，也可能因環境影響而導致運行表面損壞。

滾動表面會導致材料疲勞，從而損壞軌道和滾動元件（點蝕）。如果已知滾動接觸表面上的力，則可以根據 DIN IS 281 或 DIN 636 計算疲勞使用壽命。運行表面的磨損特別取決於潤滑、污垢、表面壓力和負載表面的相對運動大小。

計算的使用壽命可能會因額外的故障風險或其他方面而縮短，這會使保固失效。

以下各節將說明如何計算疲勞使用壽命。由於不可確定的因素，沒有標準的磨損壽命計算程序。

4.8.2 計算使用壽命 Calculating service life

4.8.2 計算使用壽命

確定外部力與力矩

作用在導軌系統上的外力由力分量 F_ax、F_ay 和 F_az，以及力作用點座標 X_a、Y_a 和 Z_a 決定。質量 m 具有加速度分量 a_x、a_y 和 a_z，會產生慣性力 F_mx、F_my 和 F_mz，這些慣性力作用於重心座標 X_m、Y_m 和 Z_m，從而對導軌系統施加負載。

垂直於工作台縱軸作用的力 ΣF_y、ΣF_z 由各個滑塊承受，因此必須根據滑塊的數量和位置分配到各個滑塊上。

此外，其他外部力矩 M_ax、M_ay 和 M_az 也可能產生影響。這些外部力矩同樣需要分配到各個 MONORAIL 滑塊。

將力與力矩分配至各個 MONORAIL 滑塊

為了計算橫向力 F_jy 和每個滑塊 (j = 1...n) 上的拉壓力 F_jz，需要應用靜力學原理。根據導軌系統的幾何形狀和剛性，可以確定力和力矩的分配。

確定預壓與變形

SCHNEEBERGER MONORAIL 導軌的預壓等級由操作條件決定，並與導軌的精度等級有關。

作用在 MONORAIL 上的外力會導致滑塊相對於導軌產生位移。根據預壓等級和作用力的大小，這些位移會有所不同。位移的計算需要考慮導軌系統的剛性特性。

影響使用壽命計算的因素

影響使用壽命的因素包括作用在 MONORAIL 滑塊上的力、預壓等級、潤滑條件、操作溫度、污染程度以及安裝精度等。這些因素在壽命計算中必須通過適當的修正係數來考慮。

動態當量力 P

為了計算使用壽命，需要確定每個 MONORAIL 滑塊 (j = 1…n) 的動態當量力 P_j。動態當量力的計算方式如下：

在 MONORAIL 滑塊承受變動負載的應用中，當力超過預壓力的 3 倍時，需要使用不同的計算方法。以下圖示說明了變動負載的情況：

然後可使用以下公式計算動態當量力 P_j 的近似值：

如果力 P 不是恆定的，則階段負載下的動態當量力 P_j 可按以下方式計算：

動態負載容量 C

滾子導軌的負載容量數據基於 DIN ISO 14728-2 所規定的原則。動態負載容量 C 是指在相同操作條件下，一組相同的導軌系統中 90% 的系統在出現疲勞損壞（點蝕）之前可以達到或超過 100 km 的額定行程距離所對應的負載。

負載容量的比較

其他製造商通常以 50 km 的行程距離為基準標示其負載容量。為了與 SCHNEEBERGER 的負載容量進行比較，可使用以下換算公式：

滾子導軌：C_100km = C_50km × 2^0.3 ≈ C_50km × 1.23

滾珠導軌：C_100km = C_50km × 2^1/3 ≈ C_50km × 1.26

事件機率

根據 DIN ISO 標準，滾動接觸軸承的負載容量是針對 90% 的事件機率（可靠度）規定的。這意味著在一組相同的導軌系統中，有 90% 的系統可以達到或超過計算的額定壽命。對於更高的可靠度要求，可使用修正係數 a₁：

使用壽命計算

對於當量力 P (N) 和動態負載容量 C (N)，標稱計算壽命 L_nom 可按以下方式計算：

使用壽命公式
Lnom	標稱壽命 (km)
C	動態負載容量
P	當量力
a1	壽命調整係數
q	使用壽命計算指數
	= 10/3（滾子型）
	= 3（滾珠型）

壽命也可以用運行小時數表示。為此，需要考慮平均速度和使用係數：

運行小時數計算
Lh	標稱壽命（小時）
s	行程長度 (m)
nh	每小時循環次數

注意事項

4.8.3 計算 S0 Calculating S0

4.8.3 計算靜態可信賴性係數 S₀

靜態可信賴性係數 S₀ 是防止滾動元件和軌道產生不允許的永久變形的安全保障，定義為靜態負載能力 C₀ 與靜態等效力 P₀ 的比值。

符號說明

S₀靜態可信賴性係數

C₀靜態負載能力

P₀靜態等效力

F_0y外部靜態力 (N)

F_0z外部靜態力 (N)

M_0QL允許的靜態縱向或橫向力矩 (Nm)

M₀靜態力矩負載 (Nm)

對於 P₀，必須考慮作用在滾動接觸表面上的實際力。滾動接觸表面變形的決定性因素是最高振幅，即使只是在很短的時間內發生。根據要求和操作條件，我們建議遵守以下靜態可信賴性係數 S₀ 的最小值：

4.8.4 計算程式 Calculation program

4.8.4 MONORAIL 尺寸計算程式

手動計算使用壽命、可信賴性因子，特別是組合負載下的位移，非常複雜，只能用於簡單應用。因此，SCHNEEBERGER 提供使用電腦程式進行計算的服務。

MONORAIL 計算程式的目的與用途

電腦輔助計算程式用於 MONORAIL 的尺寸設計，可確定以下項目:

• 所需的 MONORAIL 尺寸
• 最佳預壓
• 靜態可信賴性因子
• 額定使用壽命
• 在給定 MONORAIL 系統中，工作點在負載作用下的撓度

計算時考慮各個 MONORAIL 滑塊的真實非線性剛性，以及由拉伸、壓縮和橫向負載下不同剛性所產生的滑塊之間的相互作用。不考慮由於熱膨脹和機器結構彈性變形而產生的額外變形。

所需資料

作為設計範例，需要完整的資料，如下一頁的機械圖和資料表所示:

• 導軌幾何形狀，包括滑塊和導軌數量、滑塊縱向和橫向間距
• 空間中軸的位置以及軸之間的距離(相鄰軸參考點之間的距離)
• 所有被計算的機器軸和工件的質量
• 質量重心位置
• 驅動元件相對於相應軸參考點的位置
• 負載點位置(力和力矩的作用點)
• 所有被計算軸的最大行程(衝程)
• 軸的最大速度和加速度

此外，對於不同的負載情況:

• 集體負載，包括速度、加速度、行程距離和時間百分比，以及根據相應負載情況在工作點施加的力和力矩的大小和方向

所有幾何尺寸均與相應的軸中心相關(參見圖面)。笛卡爾坐標系中軸的命名可根據需要選擇。

對於大量典型機器和設計，SCHNEEBERGER 可提供機器草圖和資料表。如需更多資訊，請聯繫您的 SCHNEEBERGER 代表。

4.8.5 範例數據表 Sample data sheet

4.8.5 X-Y 工作台的範例數據表

基本資料

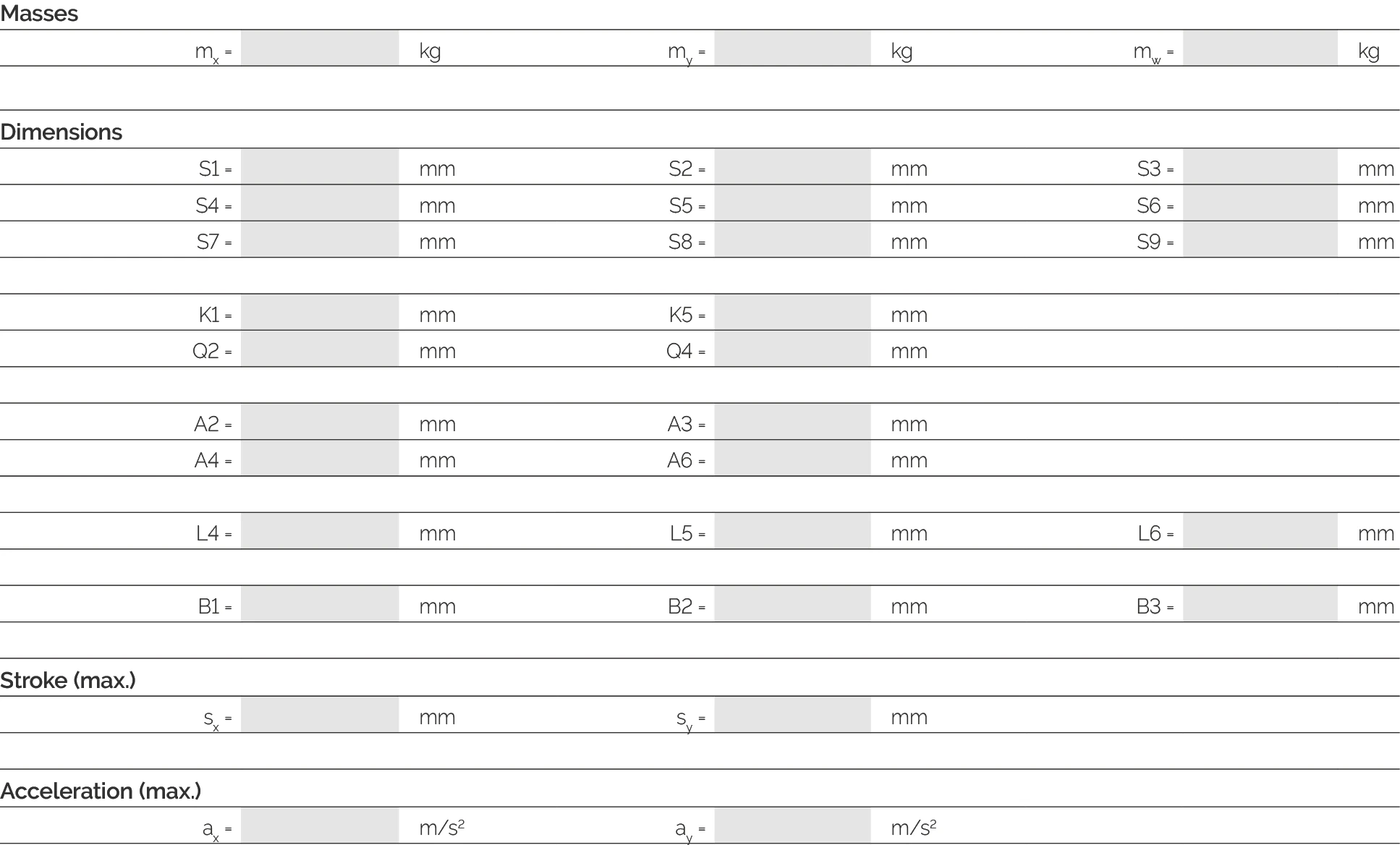
尺寸

組合力：力和力矩

組合力：距離/時間比例

4.8.6 範例機器圖紙 Sample machine drawing

4.8.6 X-Y 工作台的範例機械圖

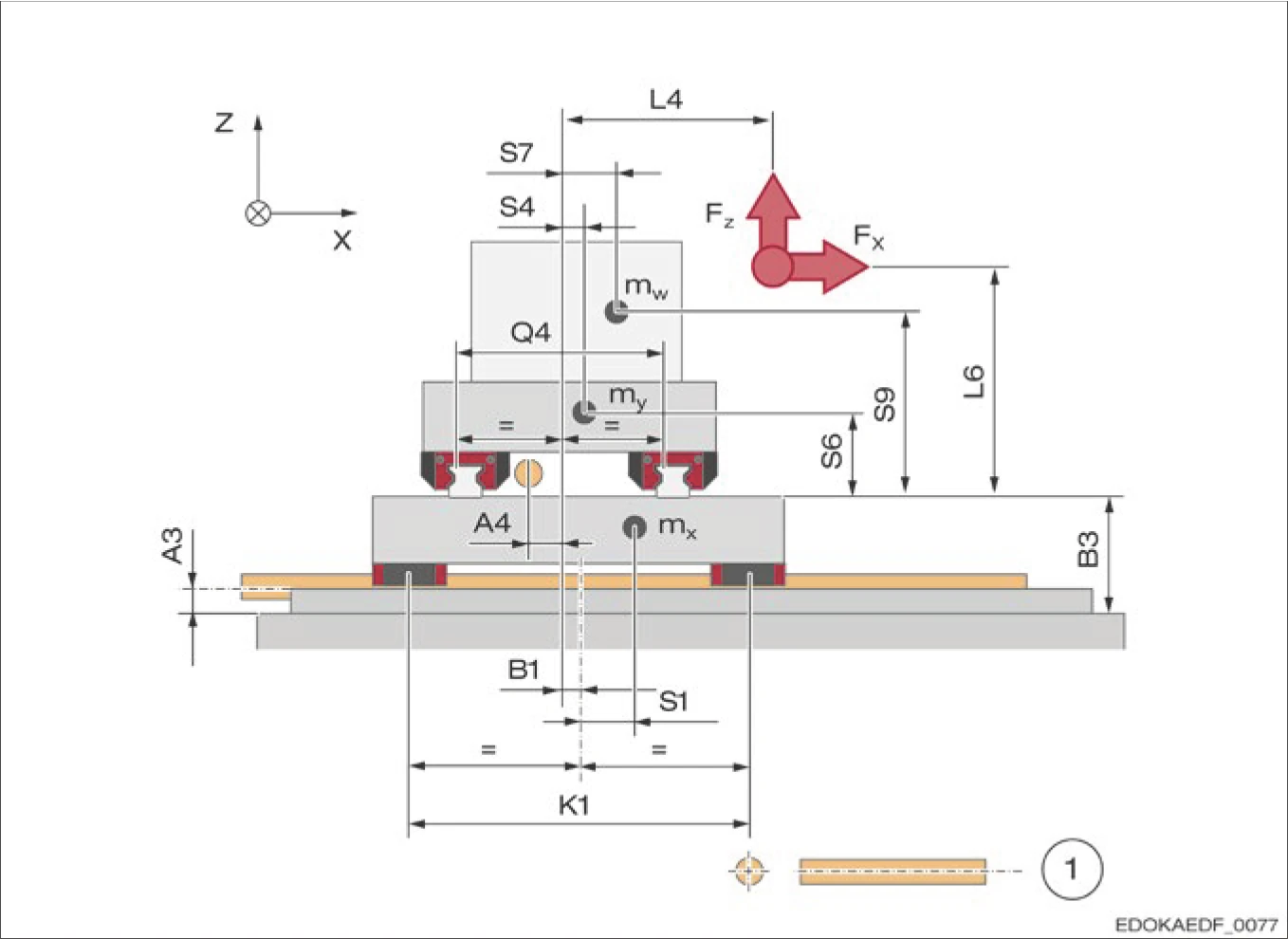
X-Y 工作台的範例機械圖
1 滾珠螺桿

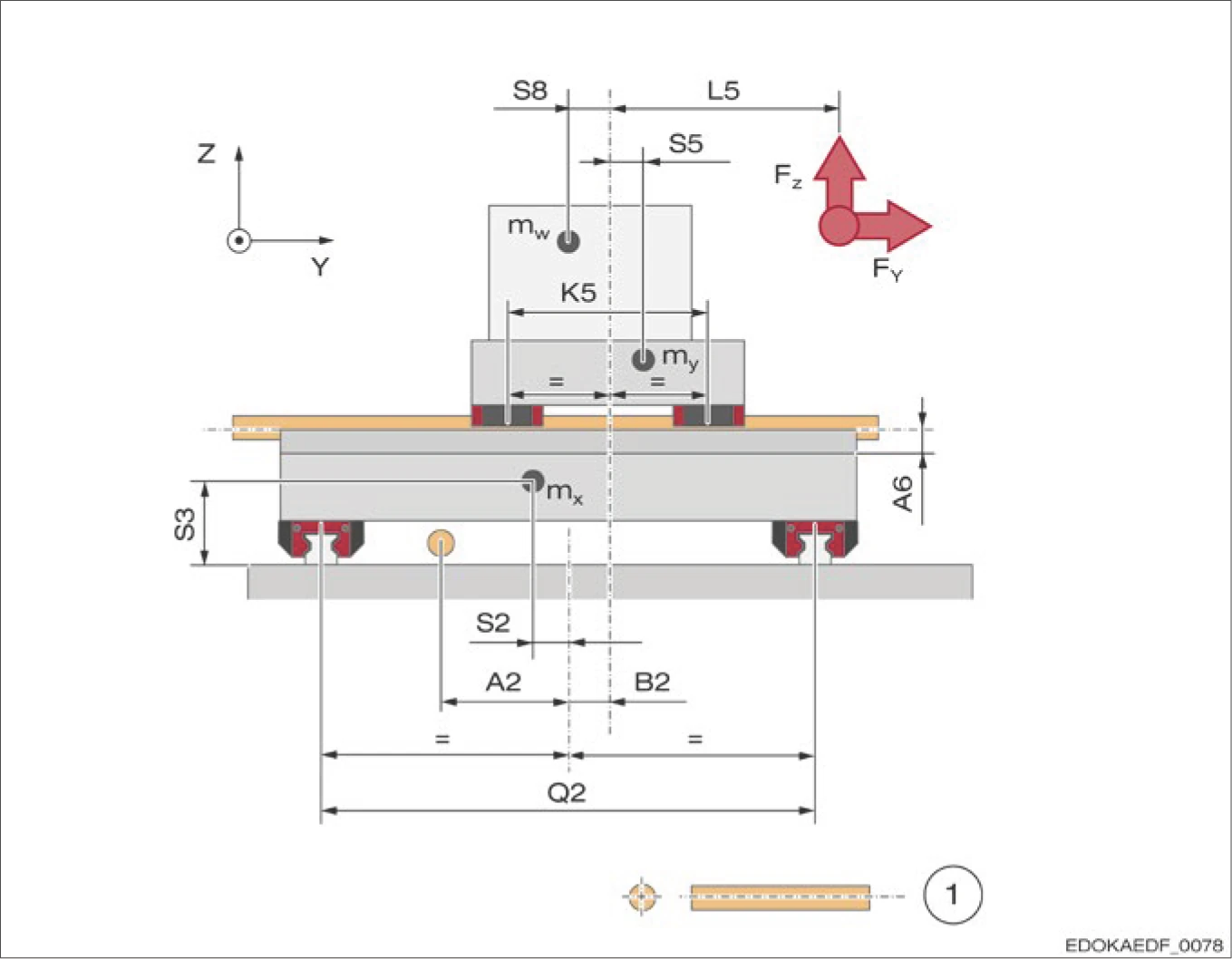
X-Y 工作台的範例機械圖
1 滾珠螺桿