17.1 原則
負載負載能力基於 DIN 636 的原則。
根據 DIN 標準,在大多數應用中,可以允許 0.0001 倍滾動元件直徑的永久總變形,而不會對軸承的操作行為產生不利影響。因此,靜態負載能力 C0 設置得足夠高,以便當等效靜態負載對應於靜態負載能力時,上述變形大約發生。建議以動態負載能力 C 為指導,以便上述總變形不會發生。
動態負載能力 C 是指在名義使用壽命 L 為 100 km 行程距離時達到的負載。在計算使用壽命時,重要的是要注意,不僅要考慮垂直作用於導軌上的負載,還要考慮所有作用力和力矩的負載譜。
使用壽命對應於導軌在任何一個滾動導軌元件上出現明顯材料疲勞之前所能達到的總行程距離(以米為單位)。當 90% 的相同結構的導軌在正常操作條件下達到或超過相應的行程距離時,即達到名義使用壽命。
對於導軌尺寸確定的關鍵因素是與動態負載能力 C 成正比出現的負載。
目錄中給出的動態負載能力 C 對應於 (≙) C100 的定義。
使用壽命定義
如前所述,動態負載能力 C100 基於 100 km 的使用壽命。其他製造商經常為 50 km 的使用壽命指示負載能力 C50。由此產生的負載能力比 DIN ISO 標準規定的高出 20% 以上。
滾珠軸承的轉換示例
根據 DIN ISO 標準將 C50 負載能力轉換為 C100:
C100 = 0.79 · C50
將 C100 負載能力轉換為 C50:
C50 = 1.26 · C100
C50 = 50 km 行程距離的動態負載能力 C(單位:N)
C100 = 100 km 行程距離的動態負載能力 C(單位:N),根據 DIN ISO 標準定義
17. 負載負載能力和使用壽命
17.2 根據 DIN ISO 標準計算使用壽命 L
17.2.1 滾珠導軌名義使用壽命計算公式(以米為單位)如下:
L = a · (Ceff / P)3 · 105 m
a = 事件概率係數
Ceff = 有效負載負載能力 N
P = 動態等效負載 N
L = 名義使用壽命 m
事件概率係數 a
滾動接觸軸承的負載負載能力符合 DIN ISO 標準。這代表使用壽命計算中的一個值,在導軌的操作使用期間有 90% 的機會被超越。
如果前述的理論使用壽命概率係數 90% 不足夠,則需要使用係數 a 調整使用壽命值。
| 事件概率 (%) Event probability in % | 90 | 95 | 96 | 97 | 98 | 99 |
|---|---|---|---|---|---|---|
| 係數 a Factor a | 1 | 0.62 | 0.53 | 0.44 | 0.33 | 0.21 |
17.2.2 以小時為單位計算名義使用壽命的公式如下:
Lh = L / (60 · vm) = L / (2 · s · n · 60)
L = 名義使用壽命 m
Lh = 名義使用壽命 h
s = 行程長度 m
n = 行程頻率 min-1
vm = 中等行駛速度 m/min
17.2.3 有效負載負載能力 Ceff
結構性和外部影響可能會降低 MINI-X 產品的動態負載能力 C,因此必須計算 Ceff。
Ceff = fK · C
Ceff = 有效負載負載能力 N
fK = 接觸係數
C = 最大允許動態負載負載能力 N
接觸係數 fk
如果多個滑塊以最小間距(Lb < L)背靠背安裝,由於導軌元件和安裝表面的製造公差,將難以實現均勻的重量分配。可以使用接觸係數 fk 來考慮這種安裝情況:
| 滑塊數量 Number of carriages | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 接觸係數 fk Contact factor fk | 1 | 0.81 | 0.72 | 0.66 | 0.62 |
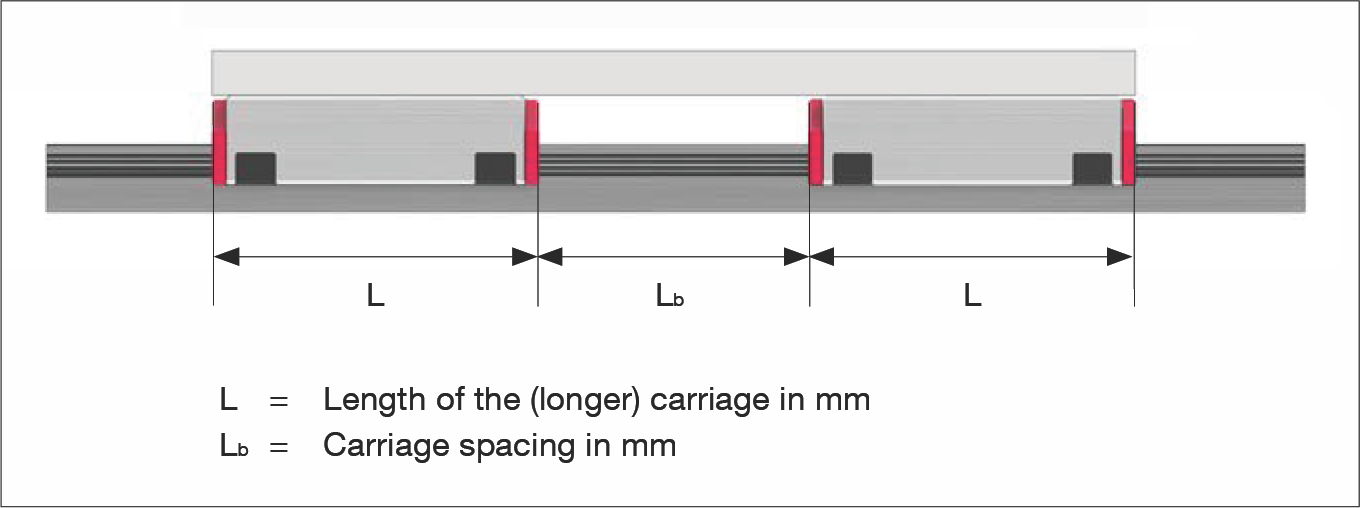
L = 滑塊長度(較長滑塊)mm
Lb = 滑塊間距 mm
17.2.4 動態等效負載 P
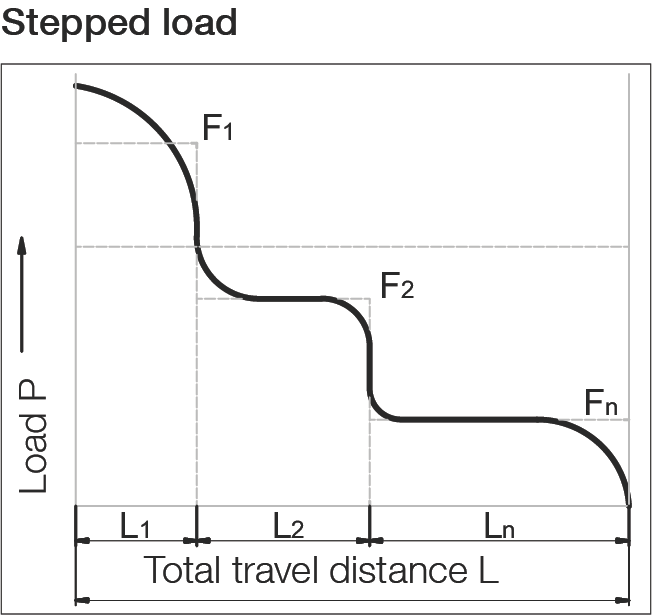
作用於線性導軌系統的負載(F)在操作期間會頻繁波動。在計算使用壽命時應考慮這種情況。導軌在行程距離期間不同操作條件下的變化負載吸收被描述為動態等效負載 P。
P = ³√[(F₁³ · L₁ + F₂³ · L₂ + ... + Fₙ³ · Lₙ) / L]
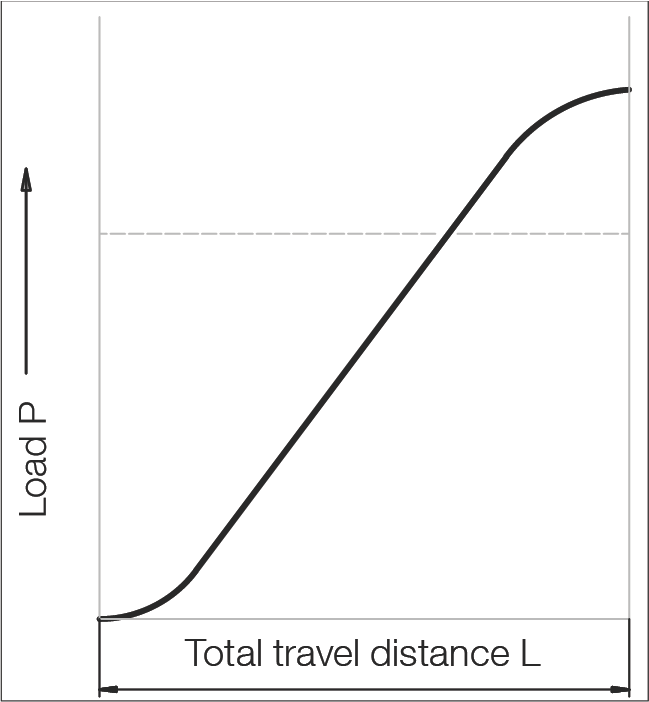
正弦負載
P = 0.7 Fmax
P = 等效負載 N
F₁ ... Fₙ = 在部分行程距離 L₁ ... Lₙ 期間的單個負載 N
Fmax = 最大負載 N
L = L₁ + ... + Lₙ = 一個負載週期內的總行程 mm
L₁ ... Lₙ = 負載週期期間單個負載的部分行程距離 mm