Service Life Calculation Formulas
For Rollers and Needles
For Balls
a = Event probability factor
Ceff = Effective load carrying capacity per rolling element (N)
P = Dynamically equivalent load (N)
L = Nominal service life (m)
Event Probability Factor a
The load capacity of roller contact bearings conforms to DIN ISO standards. This represents a value in the service life calculation that has a 90% probability of being exceeded during the operational use of the guideway.
If the previously mentioned theoretical service life probability factor of 90% is not sufficient, the service life value needs to be adjusted by factor a.
| Event Probability (%) | 90 | 95 | 96 | 97 | 98 | 99 |
|---|---|---|---|---|---|---|
| Factor a | 1 | 0.62 | 0.53 | 0.44 | 0.33 | 0.21 |
Effective Load Carrying Capacity Ceff
External influences (such as track hardness and temperature) may reduce the load capacity C, which means Ceff needs to be calculated.
Ceff = Effective load carrying capacity per rolling element in N
fH = Hardness factor
fT = Temperature factor
C = Max. permissible load carrying capacity per rolling element in N
Hardness Factor fH
Materials deviating from the standard conditions (HRC 58-62) in friction-free guideways can be recorded with factor fH:
| Track Hardness (HRC) | 20 | 30 | 40 | 50 | 55 | 56 | 57 | 58-62 |
|---|---|---|---|---|---|---|---|---|
| Hardness factor fH | 0.1 | 0.2 | 0.3 | 0.6 | 0.8 | 0.88 | 0.95 | 1 |
Temperature Factor fT
Increased temperature affects operating conditions (material properties) and must be considered using factor fT.
| Guideway Temperature (°C) | ≤ 150 | 200 | 250 | 300 |
|---|---|---|---|---|
| Temperature factor fT | 1 | 0.9 | 0.75 | 0.6 |
Ceff Calculation Example
Given Conditions:
- Guideway type R6
- Hardness 58-62 HRC ⇒ fH = 1
- Temperature 200°C ⇒ fT = 0.9
- Cage AA 6 ⇒ C = 530 N (per roller)
Dynamically Equivalent Load P
The load (F) acting on the linear guideway system is subject to frequent fluctuations during operation. This situation should be considered when calculating service life. The different load absorption of the guideway under different operating conditions during the travel distance is described as the dynamically equivalent load P.
Stepped Load
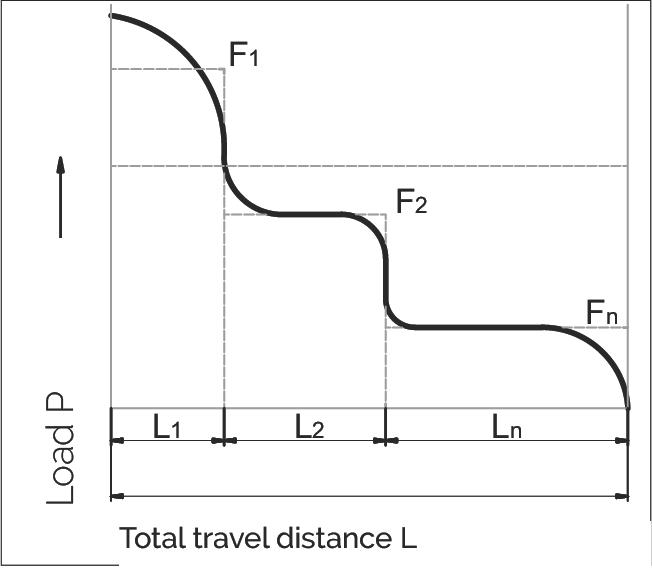
For rollers and needles:
For balls:
Sinusoidal Load
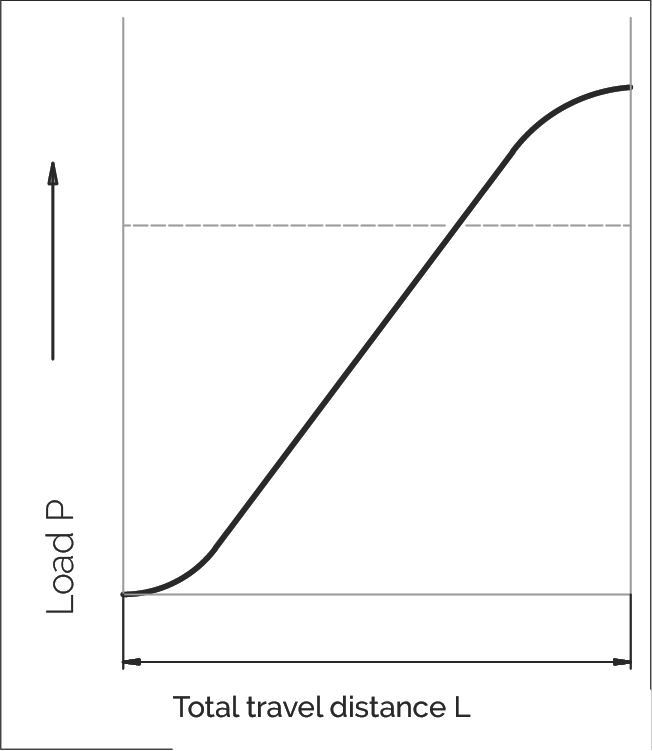
P = Equivalent load (N)
F₁...Fn = Individual loads during partial travel distances L₁...Ln (N)
Fmax = Maximum load (N)
L = L₁ + ... + Ln = Total travel during one load cycle (mm)
L₁...Ln = Partial travel distances during load cycle for individual loads (mm)
Service Life Calculation Example
Example: RNG 6-300 Linear Guideway with KBN 6 Cage
1. Given Conditions
| Event Probability | 97%, corresponding factor a = 0.44 |
| Dynamic Load Capacity per Roller | 1,800 N |
| Number of Rollers | 16 |
| Total Guideway Load Capacity | 16 × 1,800 N = 28,800 N |
| Applied Load | P = 10,000 N |
2. Service Life Calculation in Meters
Using the formula:
Substituting values:
Calculation Result:
L = 1,495,412 m
Service life ≈ 1.5 million meters
3. Conversion to Operating Hours
If service life needs to be expressed in hours, the following parameters are required:
- H = Distance per stroke (meters)
- t = Time to complete one stroke (seconds)
Service life (hours) calculation formula:
Correction Factor Rtmin
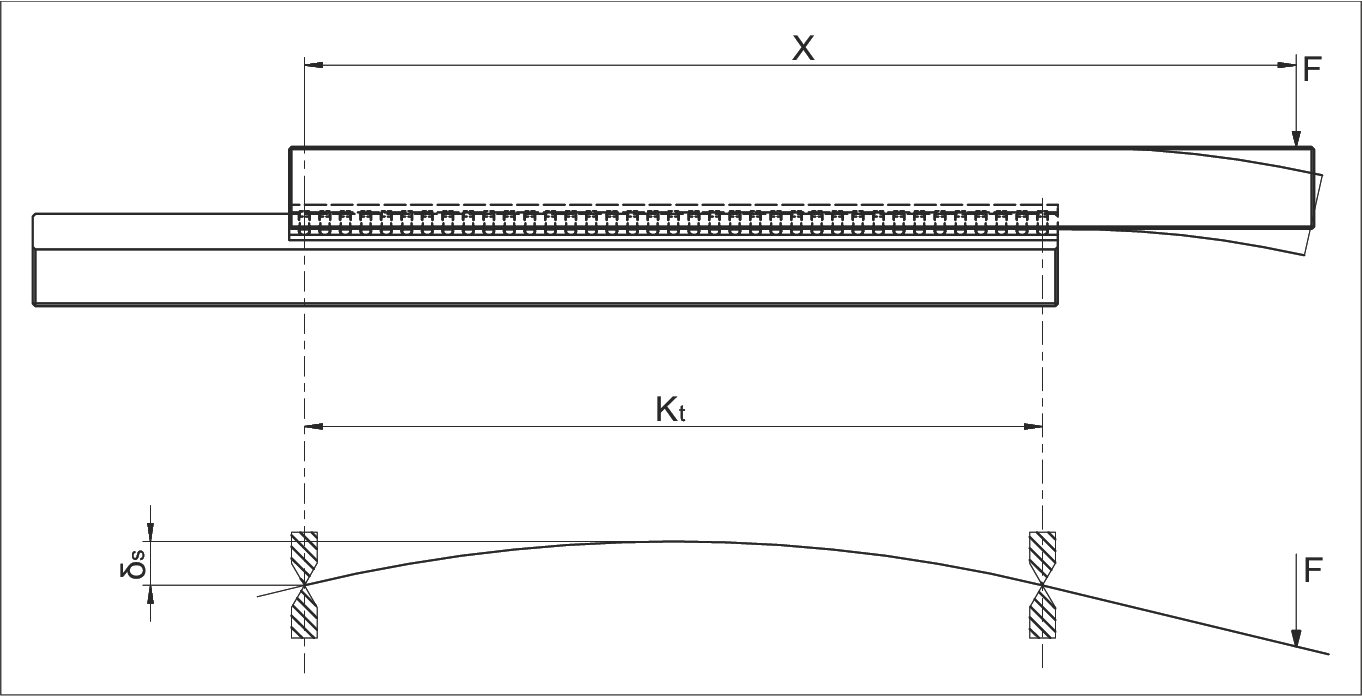
In the previous sections, we explained how to calculate service life based on given load capacity and actual load. In this process, the number of load-bearing rolling elements (Rt) per cage must be considered.
Equally important is evaluating the behavior of the surrounding structure in transmitting forces to the friction-free guideway. Elastic deformation or geometric errors in the machine tool result in only a portion of the installed rolling elements effectively absorbing the load.
Determining Rtmin
To determine Rtmin, the rigidity of the connecting structure must first be evaluated based on historical experience:
A = Rigid Structure
B = Normal Structure
Parameter Definitions
| δS | Deformation of the connecting structure in µm |
| δA | Deformation of the rolling element including the guide rail in µm (see chapter 12.5) |
| F | Load in N |
| X | Lever arm distance on x-axis in mm |
| Kt | Load-bearing cage length in mm |
| Rt | Number of load-bearing rollers |
| Rtmin | Correction factor |
Rtmin Calculation Chart
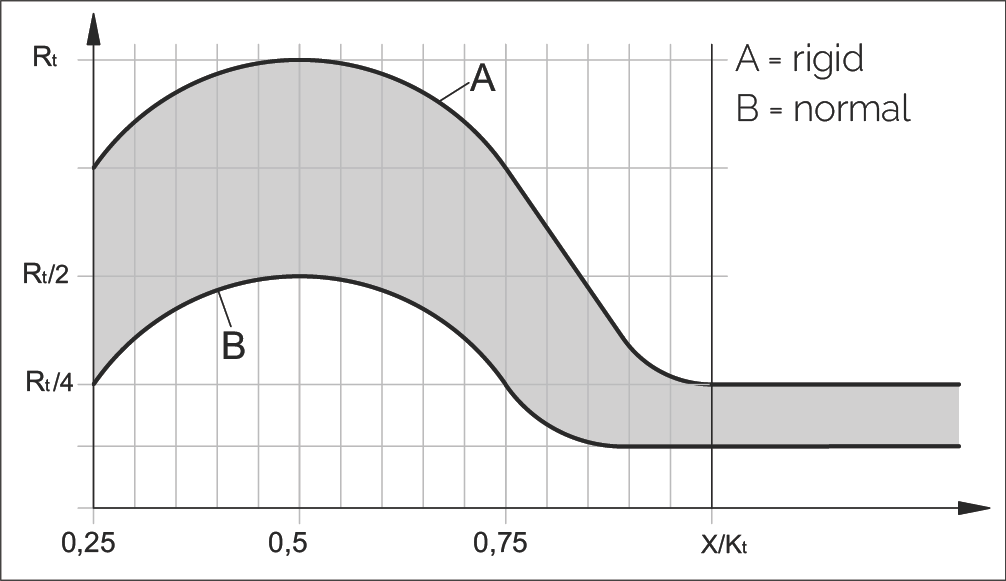
Chart Description:
- Curve A: Rigid structure
- Curve B: Normal structure
- X-axis: X/Kt ratio
- Y-axis: Rt value (Rt/2, Rt/4, etc.)
Rtmin Values for Different Rolling Element Types
| For Rtmin, the following applies | Rolling Element Type | Cage Types |
|---|---|---|
| 2 | Balls | AK |
| 1 | Rollers | AA, AC, EE, KBN and KBS |
| 5 | Needles | SHW and HW |
| 0.5 | Recirculating unit with rollers | SR and NRT |
| 1 | Recirculating unit with balls | SK, SKD and SKC |