17.1 Principles
Load carrying capacity is based on the principles of DIN 636.
According to DIN standards, in most applications, a permanent total deformation of 0.0001 times the rolling element diameter can be permitted without adversely affecting the operating behavior of the bearing. Therefore, the static load capacity C0 is set high enough so that the above deformation approximately occurs when the equivalent static load corresponds to the static load capacity. It is recommended to use the dynamic load capacity C as a guide so that the above total deformation does not occur.
The dynamic load capacity C is the load achieved at a nominal service life L of 100 km travel distance. When calculating service life, it is important to note that not only the load acting vertically on the guideway must be considered, but also the load spectrum of all acting forces and moments.
Service life corresponds to the total travel distance (in meters) that the guideway can achieve before obvious material fatigue occurs on any one rolling guideway element. The nominal service life is reached when 90% of guideways of the same construction reach or exceed the corresponding travel distance under normal operating conditions.
The critical factor for guideway sizing is the load appearing proportional to the dynamic load capacity C.
The dynamic load capacity C given in the catalog corresponds to (≙) the definition of C100.
Service Life Definition
As previously mentioned, the dynamic load capacity C100 is based on a service life of 100 km. Other manufacturers often indicate load capacity C50 for a service life of 50 km. This results in a load capacity more than 20% higher than that specified by the DIN ISO standard.
Conversion Example for Ball Bearings
Convert C50 load capacity to C100 according to DIN ISO standard:
C100 = 0.79 · C50
Convert C100 load capacity to C50:
C50 = 1.26 · C100
C50 = Dynamic load capacity C for 50 km travel distance (unit: N)
C100 = Dynamic load capacity C for 100 km travel distance (unit: N), defined according to DIN ISO standard
17. Load Carrying Capacity and Service Life
17.2 Calculating Service Life L According to DIN ISO Standard
17.2.1 The formula for calculating the nominal service life of ball guideways (in meters) is as follows:
L = a · (Ceff / P)3 · 105 m
a = Event probability factor
Ceff = Effective load carrying capacity N
P = Dynamic equivalent load N
L = Nominal service life m
Event Probability Factor a
The load carrying capacity of rolling contact bearings conforms to DIN ISO standards. This represents a value in the service life calculation with a 90% chance of being exceeded during the operational use of the guideway.
If the aforementioned theoretical service life probability factor of 90% is not sufficient, the service life value must be adjusted using factor a.
| Event probability (%) | 90 | 95 | 96 | 97 | 98 | 99 |
|---|---|---|---|---|---|---|
| Factor a | 1 | 0.62 | 0.53 | 0.44 | 0.33 | 0.21 |
17.2.2 The formula for calculating nominal service life in hours is as follows:
Lh = L / (60 · vm) = L / (2 · s · n · 60)
L = Nominal service life m
Lh = Nominal service life h
s = Stroke length m
n = Stroke frequency min-1
vm = Medium travel speed m/min
17.2.3 Effective Load Carrying Capacity Ceff
Structural and external influences may reduce the dynamic load capacity C of MINI-X products, so Ceff must be calculated.
Ceff = fK · C
Ceff = Effective load carrying capacity N
fK = Contact factor
C = Maximum permissible dynamic load carrying capacity N
Contact Factor fk
If multiple carriages are installed back-to-back with minimum spacing (Lb < L), uniform weight distribution will be difficult to achieve due to manufacturing tolerances of the guideway elements and mounting surfaces. The contact factor fk can be used to account for this installation situation:
| Number of carriages | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Contact factor fk | 1 | 0.81 | 0.72 | 0.66 | 0.62 |
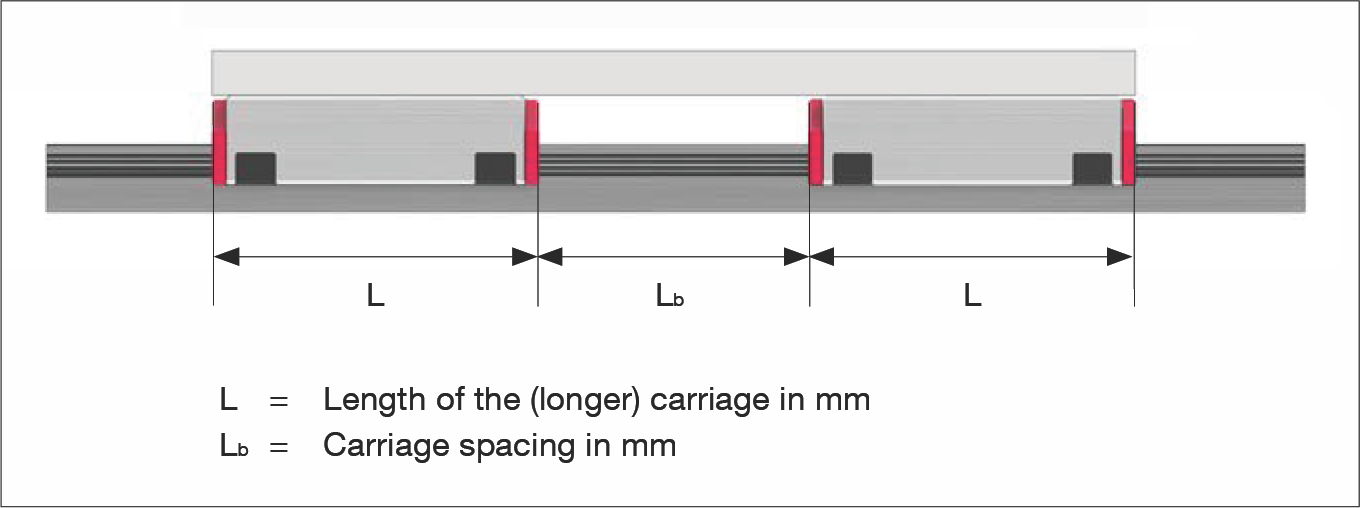
L = Carriage length (longer carriage) mm
Lb = Carriage spacing mm
17.2.4 Dynamic Equivalent Load P
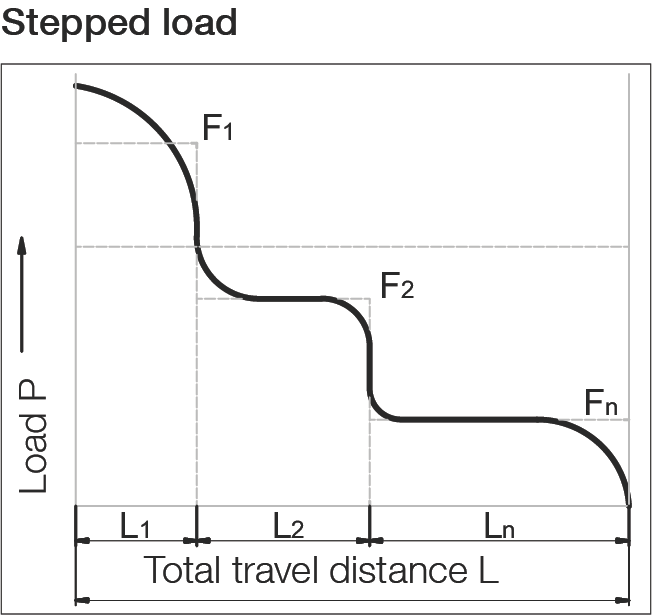
The load (F) acting on the linear guideway system frequently fluctuates during operation. This situation should be considered when calculating service life. The variable load absorption of the guideway under different operating conditions during travel distance is described as dynamic equivalent load P.
P = ³√[(F₁³ · L₁ + F₂³ · L₂ + ... + Fₙ³ · Lₙ) / L]
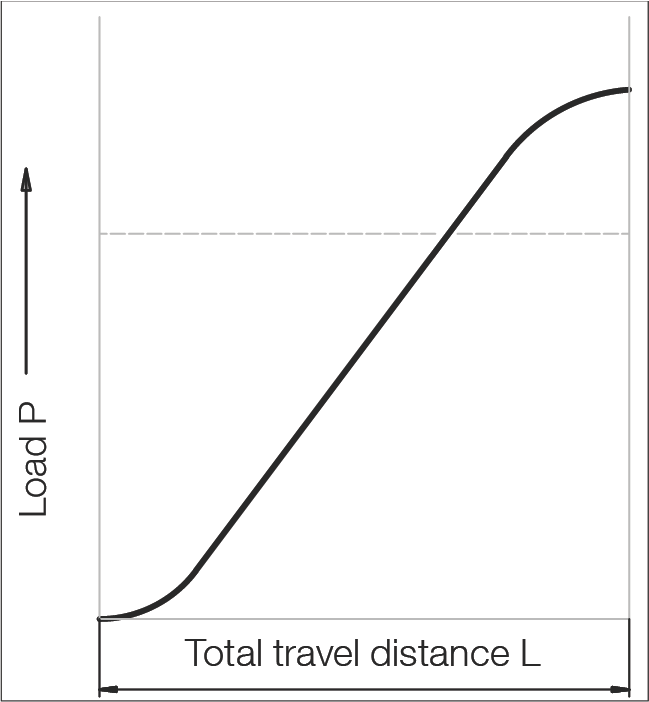
Sinusoidal Load
P = 0.7 Fmax
P = Equivalent load N
F₁ ... Fₙ = Individual loads during partial travel distances L₁ ... Lₙ N
Fmax = Maximum load N
L = L₁ + ... + Lₙ = Total travel in one load cycle mm
L₁ ... Lₙ = Partial travel distances of individual loads during load cycle mm